
HOME KS1 KS2 KS3 GCSE UNIVERSITY BUSINESS STUDIES DAY-TO-DAY IT SKILLS PERSONAL MANAGEMENT SAFARI AFRICA
© theknowledgeland.co.uk 2016





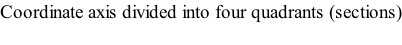
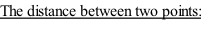



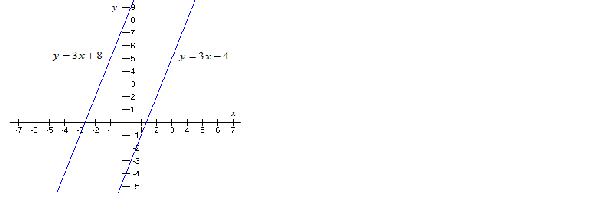






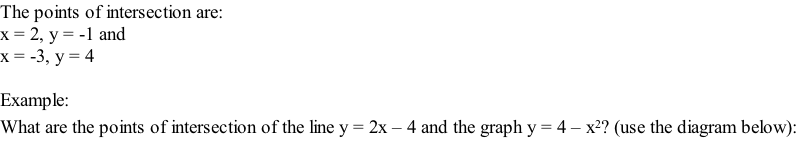

| KS2 MATH |
| MATHYEAR 4 |
| MATHYEAR 5 |
| MATHYEAR 6 |
| COUNTING TO 100,000 |
| ADDING AND TAKING AWAY |
| MULTIPLICATIONS AND DIVISIONS |
| PROBLEMS SOLVING |
| FRACTIONS |
| ROUNDING NUMBERS |
| ARITHMETIC |
| KNOW NUMBERS TO 1,000,000,000 |
| ADDITIONS AND SUBTRACTIONS |
| PROBLEM SOLVING I |
| PROBLEM SOLVING II |
| ROUNDING AND DECIMALS |
| FRACTIONS, DECIMALS AND PERCENTAGES |
| DATA HANDLING |
| PROBABILITY |
| ARITHMETICS |
| KS3 MATH |
| ARITHMETICKS3 |
| ALGEBRAKS3 |
| MEASUREMENTS AND SHAPESKS3 |
| DATA HANDLINGKS3 |
| MATHEMATICAL SIGNS |
| NUMBER LINES |
| BODMAS |
| ESTIMATIONS |
| FACTORS AND MULTIPLES |
| SQUARES AND CUBES |
| INDICES |
| FRACTIONS, DECIMALS AND PERCENTAGES |
| RATIOS AND PROPOTIONS |
| MEASUREMENTS |
| TWO DIMENSIONAL SHAPES |
| THREE DIMENSIONAL SHAPES |
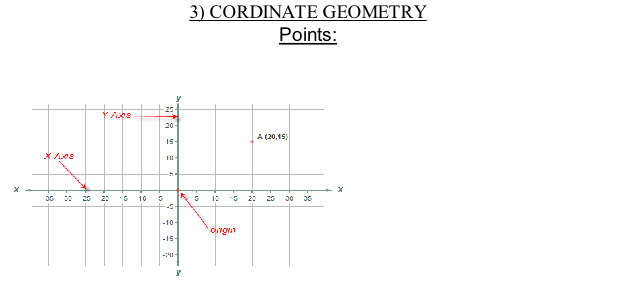
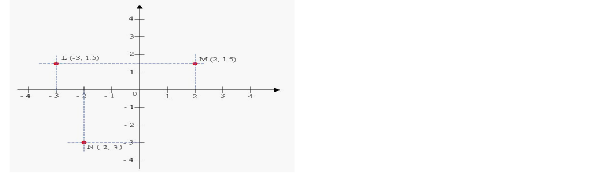
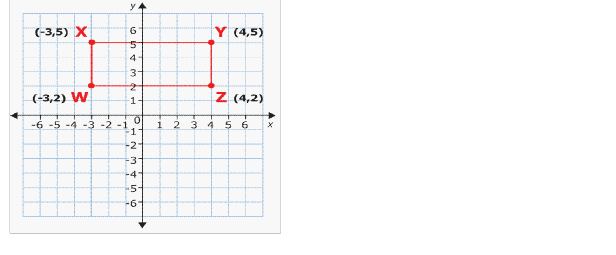
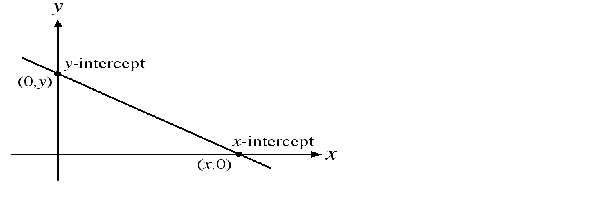
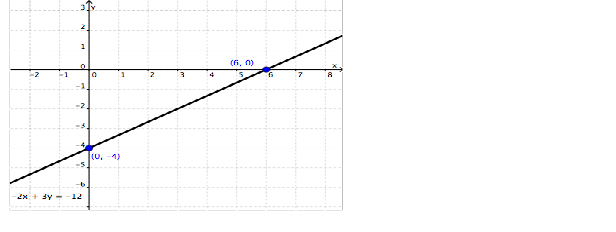
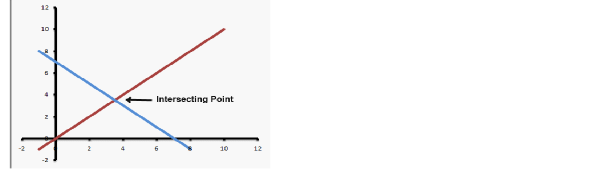
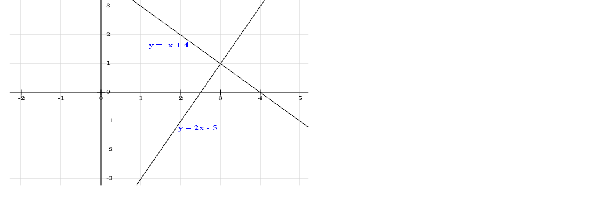
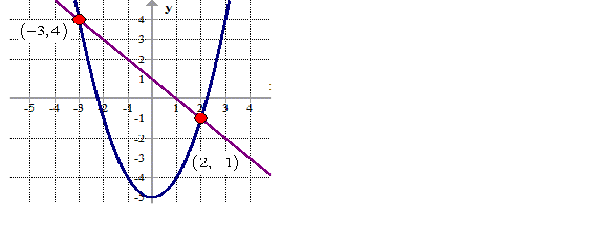
| COORDINATE GEOMETRY |
| TRIGONOMETRY |
| DATA COLLECTING AND ORGANISING |
| STATISTICAL TERMININOLOGIES |
| PICTOGRAMS |
| PIE CHARTS |
| BAR CHARTS |
| FREQUENCY POLYGONS |
| LINE GRAPHS |
| CUMULATIVE FREQUENCY POLYGONS |
| SCATTER DIAGRAMS |
| PROBABILITIES |
| ANSWERS |